Project M03 - Functional Electromagnetic Signatures from Complex Surface Systems and In-door Scenarios
Principal Investigator: Prof. Dr. Daniel Erni, UDE
Achieved Results in the 1st Phase
Introduction The central objective of project M03 was to develop a parametrizable multiscale EM model of the surface system and to carry out comprehensive simulations with respect to the sensitivity and specificity of mm-wave/THz reflectometry set-ups against constituents and textures of the underlying composite surface structure. Using human skin as one of the most challenging and meaningful testcases for complex, frequency-dependent surface composites our multiscale EM model has revealed quantitative validity limits as upper bounds for the operating frequency, which have been ignored so far in contemporary standard [1], partially multiscale [2], and multiscale [6] tissue models. These validity limits provided in addition new strategies to improve the sensitivity in surface reflectometry that are exploited using machine learning and thus enabled the classification of sub-surface features [7,8]. From a comprehensive numerical EM analysis of rough surface scattering [9], we have clarified that a coarse discretization of the surface geometry within a Finite-Difference Time-Domain (FDTD) scheme may have an astonishing low impact on the accuracy of the field solution as the stochastic approximation error may itself contribute to the rough surface model. This gives rise to potentially much simpler stochastic FDTD implementations (that also work for large perturbations) compared to modern stochastic S-FDTD schemes where the latter adopts auxiliary equations to approximate mean field and variance field contributions (via delta method) [3].
Parametrizable multiscale EM model In our current research we developed a numerical hierarchically organized three-stage methodology, which has been implemented in the framework of a multiscale simulation workbench to explore the scattering of EM waves from complex inhomogeneous surface systems. First, the modeling approach starts at the smallest length scale of the composite material's randomized microstructure. It then evolves step-by-step through the characteristic length scales of its inhomogeneous morphology using a numerical homogenization based on a quasi-static EM analysis that provides both the dispersive and tensorial EM material properties of the corresponding composite structure [10]. The inhomogeneous microstructure is conceptualized as a guest-host system of randomized inclusions (i.e. pores, particles, material features) in a homogeneous background material according to stochastic measures such as e.g. volume fraction, size of the inclusion, and the expected values for the separation distance, as well as the minimal distance. Second, after this bottom-up homogenization, the resulting multiscale material representation is introduced into a numerical reflectometry set-up that allows the analysis of the «spatial» and spectral response of the EM scattering for impinging EM waves at different angles of incidence. Third, due to the stochastic parametrization of the composite material model, the multiscale simulation workbench also allows to carry out corresponding Monte-Carlo analyses with respect to various output quantities [7,11]. The multiscale simulation workbench is implemented into the Finite-Element Method (FEM)-based simulation platform COMSOL Multiphysics allowing for the analysis of two (2D) or three (3D) dimensional inhomogeneous surface systems depending on the given computational resources. The 2D model of the reflectometry set-up in the simulation workbench operates in the frequency domain with a performance of around 81 ms/frequency point (21 s for a typical frequency response as shown in Fig.1) on a standard PC (4 Core CPU i7-6700k, 4GHz, 62GB RAM) using e.g. the MUMPS direct solver.
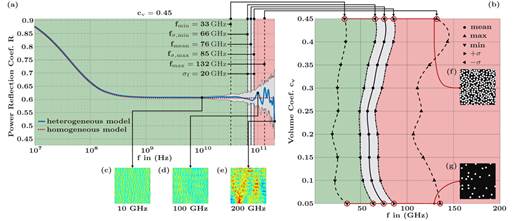
Structural analysis of composite surface systems The main goal of the envisioned numerical multi-scale modeling is to forecast and quantify the sensitivity (i.e. against constituents, shapes, patterns, and perturbations) and specificity (with respect to characterization/classification) of the underlying composite material surface from reflectometry data. As an instructive example, we, e.g., explored a generic hypodermis (HYP) tissue layer [10] as the analysis of biological tissues can be regarded as one of the most meaningful benchmark problems with respect to the EM simulation and characterization of composite material systems at mm-wave/THz frequencies. Our current research has focused on the validity limits for the material homogenization [7,11] in order to e.g. provide a formal approach to the separability between surface and volume scattering [4,5]. Here, the deviation of the power reflection between the HYP structure and its homogenized Effective Material Theory (EMT) representation are simulated in the reflectometry set-up along a Monte-Carlo analysis using 1980 implementations of fictitious HYP derivatives with different volume fractions of the cellular and extracellular material, yielding expectation values and variances for the validity limits with respect to a relative deviation of 2% (Fig.1). These validity limits were found at surprisingly low frequencies around 60-80GHz, above which the EMT representation breaks down. Each hierarchically organized multiscale model topology is therefore strongly bound to a corresponding operating frequency bandwidth, which we defined a so-called dispersion class. We have shown [7,8] – using Artificial Neural Networks (ANNs) classifiers – that both frequency ranges adjacent to the frequency of the validity limit and in particular the spectral fingerprints of the tissues in the forbidden range are apt for predicting structural/morphological features such as the expected values of cell sizes and cell spacings. We even used machine learning (ANN) to predict the most sensitive band in the forbidden range for material characterization/classification [8]. In cooperation with project M02, we have carried out numerous RF measurements for characterization and validation purposes using various 3D printed artificial composites with different fillings [7,8] (including e.g. correspondingly arranged microfluidic channels). Some composites are undergoing geometrical/frequency scaling in order address the interesting ranges (dispersion class) in the frequency response of the power reflection, as the latter has to be confined to the given operating bandwidth of the measurement set-up.
Fig.1: Validity limits for several generic HYP derivatives:(a) spectral responses of the reflectance (showing the typical Maxwell-Wagner roll-off in the MHz range) of 1980 implementations for εr,1 = 80; σ1 = 0.53 S/m; εr,2 = 50; σ1 = 0.12 S/m; dinc = 50 µm, and volume fraction cv = 0.45; (b) Validity limits of the derivatives of a heterogeneous material structure (here the HYP tissue) for a 2% deviation between the heterogenous structure and its homogenized EMT representation; (c), (d), (e) examples of the electric field distribution IEI at various frequencies (i.e. at 10 GHz, 100 GHz, 200 GHz, respectively); (f), (g) examples of the analysed microstructures (i.e. for cv = 0.45 and cv = 0.05 respectively). The validity range of the EMT material model is colored in «green» while the forbidden range is marked «red» [7,11].
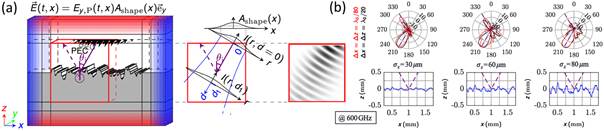
On the numerical discretization of random morphologies: The question behind this research is whether we need full resolution when discretizing a random rough surface (using e.g. a stair-case approximation in a Cartesian mesh) as the approximation error (emerging as spatial «noise» contribution) may itself support the modeling of the random rough surface. Within a very systematic study [9,12], we have approached this problem/conjecture from two sides: (i) The impact of staircasing on the proper geometry of 2D representations of the rough surface (Fig.2(a)) has been analysed. Here we used analytical self-similar Weierstrass functions for the roughness that can be parametrized by the fractal Hausdorff dimension. This figure is closely related to the Hurst exponent which shapes the decay of the associated power-density spectrum, and, hence the correlation length. (ii) The impact of staircasing on the scattered fields using a homemade 2D-FDTD computational EM simulator that fully comply to the chosen discretization. Spatial roughness functions with small (very rough) and large (weakly rough) Hurst exponents turned out to be less prone to discretization errors. The mapping of such findings into the EM scattering problem is not trivial because the definition of formal measures that allows for a quantitative comparison of (reference) scattering characteristics (retrieved from a corresponding near-to-far-field transformation of the FDTD full-wave solution) turned out to be very challenging. Nevertheless, the results shown in Fig. 2(b) are in support of the above findings: The «apparent convergence» of the scattered fields for coarse and fine discretization for the roughest surface are in accordance with the conjecture that coarse discretization of rough surfaces is feasible. Up to now, the generalization of this claim is not possible yet but part of our ongoing research, where we complement our prior Monte-Carlo analyses of various rough surface realizations with reference.
Fig.2: Discretized random surface morphologies: (a) computational domain of the discrete surface model within the homemade tailored 2D-FDTD simulator (blue and red indicate the PML boundary conditions), the red square/cube marks the analysis domain for the tilted Gaussian beam illumination with dimensions larger than the correlation length; (b) simulated far-field patterns of the reflected and transmitted (related to air) beam for increasing surface roughness and two different grid resolutions. There is a counterintuitive «apparent convergence» of the far-fields between coarse and fine discretization for the largest roughness [9].
EM FEM simulations (with unstructured meshes) of corresponding discretized rough surfaces [12] to scrutinize the emergence of the «apparent convergence». Goniometric reflection measurements from 3D printed discretized rough surfaces are now set up in collaboration with project C06 for operating frequencies between 300-400GHz. The results will be published in due course.
Slim and efficient simulation engine In this task we have worked on the development of an ultra-fast, semi-analytical computational EM simulator for (quasi-) periodic and partly irregular complex scattering structures that are applicable to e.g. the design of compact mm-wave, THz, and photonic/plasmonic devices. The current 2D frequency-domain implementation utilizes cylindrical wave expansions for each scatterer in a rigorous and thus efficient formulation based on the lattice sums (LS) technique combined with generalized reflection and transmission matrices together with a recursive algorithm for the multilayered composite structures [H,I]. A preliminary 3D implementation for multilayer composites is also available. The method is extendable to dissipative respective highly dispersive structures and complex eigenvalue problems (supporting e.g. leaky waves) when using Ewald's formulation for convergent LSs to better handle long-range evanescent field interactions in the structure, providing a further speedup of the simulation engine. The computation speedups compared to COMSOL FEM simulations are in the range of 10-15 (CPU Core i7, 3.8GHz, 32 GB RAM), depending on the exploitable periodicity of the underlying microstructure implementation where upper limits of this factor are currently estimated around 27-40. The performance of the code has been demonstrated within various applications such as e.g. complex multiple scattering systems and electromagnetic bandgap structures [13], which are applicable as building blocks for a Surface-Integrated Waveguide (SIW) technology. Examples are given for ultra-compact SIW microwave/mm-wave bandpass filters [14,15,16,17] and novel dielectric realizations of SIW waveguides and compact filters that are thus scalable up to THz frequencies [16,17]. The SIW filter design has been carried out using numerical structural optimization. The analysis of highly dispersive surface systems made of (quasi-) periodically arranged (plasmonic) volume [18] and surface [18,19] scatterers occasionally deposited onto dielectric substrates is given for optical frequencies.
Innovations and novel methods In summary, the following innovations have been achieved within this 1st project phase: (i) the quantitative estimation of validity limits for the homogenized microstructures and the derived dispersion classes regarding the operating frequency range of the overall multiscale model is new and has provided new insights into the metamaterial paradigm. (ii) Both frequency ranges adjacent to each validity limit are thus applicable in their own way for the estimation of corresponding sub-surface features. This modularized approach is new and builds upon our new criterion based on the spatial distribution of the difference in electric and magnetic energy density in the surface composite [20,8]. (iii) A further innovation concerns the strategy to apply a potentially coarse discretization to the full-wave FDTD analysis of rough surfaces [9] that goes along with a considerable speedup of the EM simulation. (iv) The present performance of the slim simulation engine [19,10] is unprecedented up to date, as it can handle complicated scattering topologies while showing ultra-fast convergence even for dissipative and dispersive settings, which allow the accurate analysis of novel dielectric SIW THz components [16,17]. This activity was very successful and even reached into the realm of nonlinear photonic crystal structures (which is actually beyond the scope the corresponding work package) with novel concepts for light wave amplification [21,22] and the very first operational bandgap soliton-based all-optical AND logic gate [22,23].
References
[1] M. C. Ziskin, S. I. Alekseev, K. R. Foster, and Q. Balzano, "Tissue models for RF exposure evaluation at frequencies above 6 GHz," Bioelectromagnetics, vol. 39, no. 3, pp. 173-189, April 2018.
[2] M. Saviz, et al., “A new open-source toolbox for estimating the electrical properties of biological tissues in the terahertz frequency band,” J. Infrared Millim. Terahertz Waves, 34(9), 529, 2013.
[3] K. Masumnia-Bisheh, et al., "Geometrically stochastic FDTD method for uncertainty quantification of EM fields and SAR in biological tissues," IEEE Trans. Antennas Propagat., 67(12), 7466, 2019.
[4] A. Sentenac, H. Giovannini, and M. Saillard, "Scattering from rough inhomogeneous media: splitting of surface and volume scattering," J. Opt. Soc. Am. A, 19(4), 727, 2002.
[5] C.-A. Guérin, A. Sentenac, "Separation of surface and volume effects in scattering from heterogeneous rough surfaces: derivation of a splitting rule," J. Opt. Soc. Am. A, 24(2), 385, 2007.
Selected Project-related publications
For all project-related publications please click here and scroll to the M03 section.
[6] J. Froehlich, S. Huclova, C. Beyer, and D. Erni, "Accurate multi-scale skin model suitable for determining sensitivity and specificity of changes of skin components," in Computational Biophysics of the Skin, Bernard Querleux (ed.), Singapore: Pan Stanford Publishing Pte. Ltd., 2014.
[7] K. Jerbic, B. Sievert, J. T. Svejda, J. Jebramcik, J. Barowski, A. Rennings, I. Rolfes, and D. Erni, "Limits of homogenization in electromagnetic composite material models: A show case in tissue analysis," IEEE Workshop 2020 and SENSORICA 2020, Mülheim a. d. Ruhr, Germany, 2020 (cf. [8]).
[8] K. Jerbic, K. Neumann, J. T. Svejda, B. Sievert, A. Rennings, and D. Erni, "Limits of effective material properties in the context of a electromagnetic tissue model," arXiv:2007.00635, (https://arxiv.org/abs/2007.00635), 2020.
[9] Benedikt Sievert, Die Rolle der Diskretisierung bei der elektromagnetischen Simulation rauer Oberflächen, Master thesis, ATE, Universität Duisburg-Essen, 2019.
[10] D. Erni, K. Jerbic, A. Rennings, S. Huclova, J. Froehlich, "Mehrskalige elektromagnetische Gewebemodelle für den mm-Wellen-Bereich," FSM-Workshop: Millimeterwellen – Stand der Forschung, Forschungsstiftung Strom und Mobilkommunikation, June 18-19, ETH Zurich, Zürich, Switzerland, 2019, (invited).
[11] K. Jerbic, B. Sievert, J. T. Svejda, A. Rennings, and D. Erni, "On the applicability of homogenization in composite material models for tissue analysis in the mm-wave range," PIERS 2019, Rome, Italy, June 17-20, 2019.
[12] Tim Toelle, Das Konvergenzverhalten durch die Diskretisierung randomisierter rauer Oberflächen bei der elektromagnetischen Simulation von Reflexionsereignissen. Bachelor thesis, ATE, Universität Duisburg-Essen, 2020.
[13] V. Jandieri, D. Erni, "Electromagnetic scattering, guidance and radiation in cylindrical periodic and bandgap structures," URSI AT-RASC 2018, Gran Canaria, Spain, May 28 – June 1, 2018.
[14] A. Akopian, G. Burduli, V. Jandieri, H. Maeda, W. Hong, A. A. Omar, K. Yasumoto, D. H. Werner, and D. Erni, "Efficient analysis of electromagnetic scattering in post-wall waveguides and its application to optimization of millimeter-wave filters," IEEE Open J. Antennas Propagat. (OJAP), 2020. (accepted)..
[15] A. Akopian, G. Burduli, V. Jandieri, H. Maeda, W. Hong, K. Yasumoto, and D. Erni, "Numerical study and optimization of post-wall waveguides and filters for millimeter waves," GeMiC 2020, Cottbus, Germany, March 9-11, 2020.
[16] E. Archemashvili, V. Jandieri, H. Maeda, K. Yasumoto, J. Pištora, and D. Erni, "Numerical analysis of dielectric post-wall waveguides," IWAT 2020, Bucharest, Romania, Feb. 25-28, 2020.
[17] V. Jandieri, K. Yasumoto, D. H. Werner, J. Pistora, and D. Erni, "Efficient design of filters based on metallic and dielectric periodic structures in SIW technology," URSI-GASS 2020, Rome, Italy, Aug. 29 – Sept. 5, 2020, (invited).
[18] V. Jandieri, K. Yasumoto, J. Pistora, and D. Erni, "Analysis of scattering by plasmonic gratings of circular nanorods using lattice sums technique," Sensors, 19(18), 3923, Sept. 11, 2019.
[19] V. Jandieri, L. Okropiridze, K. Yasumoto, D. Erni, and J. Pistora, "Efficient analysis method of light scattering by a grating of plasmonic nanorods," COMPEL, 37(4), 1436, Oct. 2018.
[20] G. Solomakha, J. T. Svejda, C. van Leeuwen, A. Rennings, A. J. Raaijmakers, S. Glybovski, D. Erni, "A self-matched leaky-wave antenna for ultrahigh-field MRI with low SAR," arXiv:2001.10410, (https://arxiv.org/abs/2001.10410), 2020.
[21] V. Jandieri, T. Onoprishvili, R. Khomeriki, and D. Erni, "Realization of linear amplification of optical signal in guiding nanostructures," PIERS 2018, Toyama, Toyama, Japan, Aug. 1-4, 2018.
[22] V. Jandieri, R. Khomeriki, D. Erni, and W. C. Chew, "Realization of all-optical digital amplification in coupled nonlinear bandgap waveguides," Prog. Electromagn. Res. (PIER), 158, 63, 2017.
[23] V. Jandieri, T. Onoprishvili, R. Khomeriki, D. Erni, and J. Pistora, "Digital signal processing in coupled photonic crystal waveguides and its application to an all-optical AND logic gate," Opt. Quant. Electron., 51(4), 121, April 2019.
[24] A. Akopian, G. Burduli, V. Jandieri, H. Maeda, W. Hong, A. A. Omar, K. Yasumoto, D. H. Werner, and D. Erni, "Efficient analysis of electromagnetic scattering in post-wall waveguides and its application to optimization of millimeter-wave filters", IEEE Open Journal of Antennas Propagatioin (OJAP), August 2020. [accepted].


